Overview

My goal for this project was to leverage image warping, registering, resampling, and compositing for visually interesting applications such as image rectification and image mosaics.

Section I: Shoot the Pictures

I took several pairs of images to stitch together and selected key points between shared features using the provided tool. To ensure that each image pair contained a projective transform, I fixed the center of projection while varying the camera angle.

Section II: Recover Homographies

Given at least four sets of points from each, I can compute the homography between two images by finding the solution to the following system of equations:

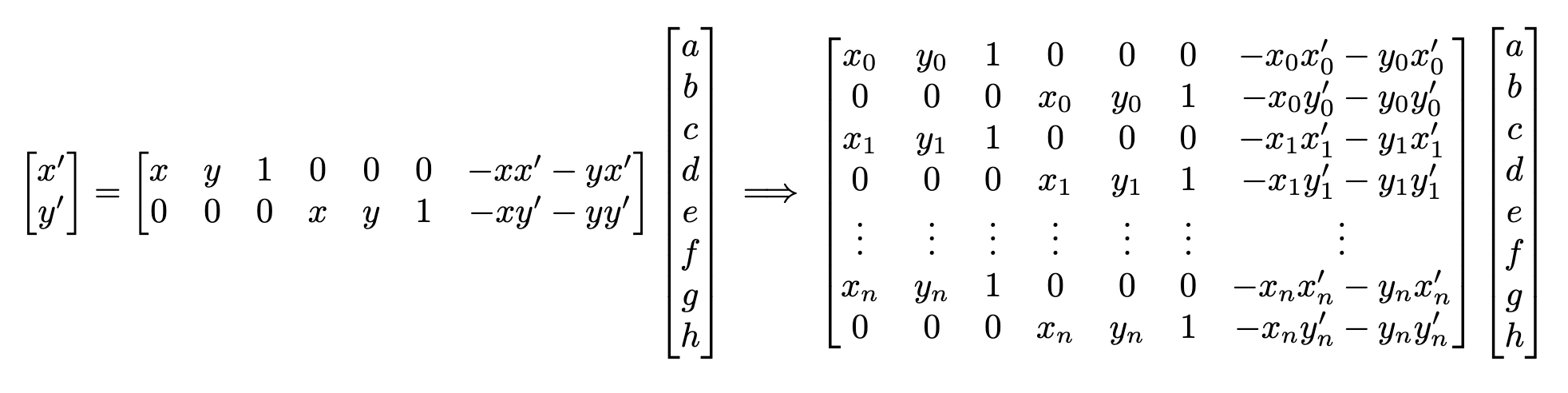
The system can be solved as follows on the left. In the case that I’m using more than four sets of points, the system becomes overdetermined and can be solved using the least squares method on the right:

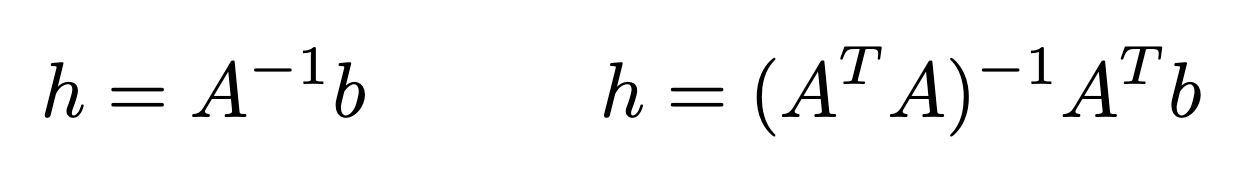
I can now construct the homography as the following 3x3 matrix using the obtained coefficients:

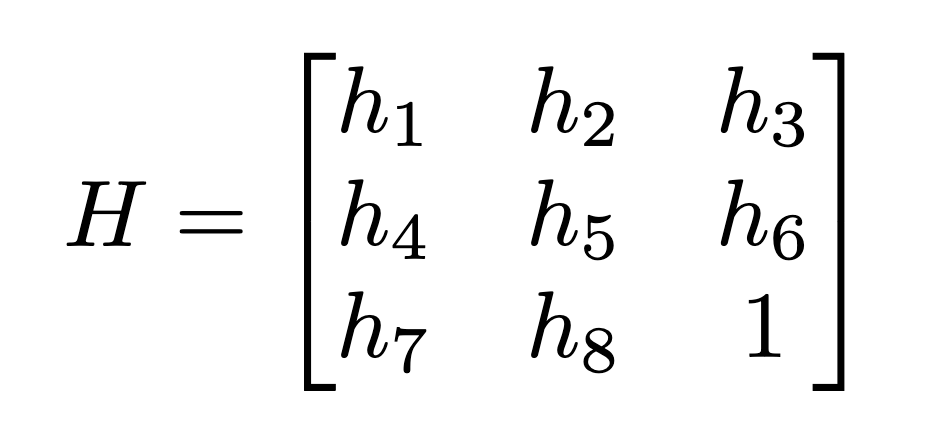
Finally, to warp the image, I apply the homography to homogenized sets of coordinates and scale the resulting coordinates by w :

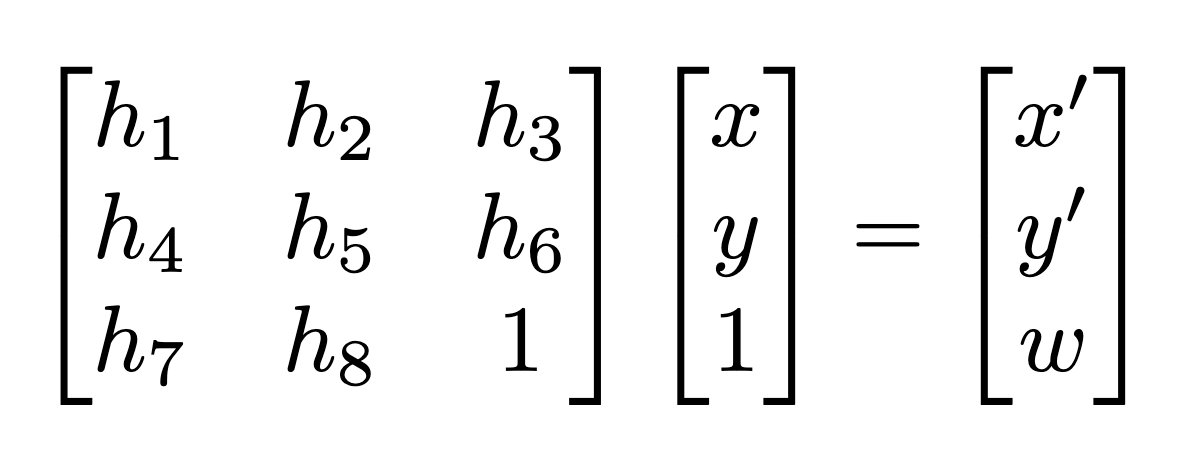
Section III: Warp the Images

Image Rectification

To test my implementation, I rectified some images by mapping a warped surface to a flat rectangular plane. First, I selected key points at each corner of the surface I wanted to rectify, then calculated the homography from the source points to the points of the desired plane. To determine the bounds of the rectified image, I warped the bounds of the source image then found the mask contained by the bounds.

I performed inverse warping by using the inverse homography to map the mask back to the source image. Finally, I used nearest neighbor interpolation to populate the pixels of the rectified image based on the source image.

As you can see in the last result, this method doesn't always succeed in emulating real-life perspective.

Blend the Images Into a Mosaic

Finally, I moved onto blending images into a mosaic. Images in the mosaic must have the same perspective, so I averaged the key points of both images to find the target plane and computed the corresponding homographies to this plane.

I based the dimensions of the final bounding box on the sum of the minimum and maximum bounds of each image (post warp). To account for these new bounds, I shifted the warped images accordingly before placing them within the bounding box. The final mosaic is defined by the simple average between the alpha masks of both images. Highly intricate structures like the ribcage are still a bit blurry even after the warp, which could likely be improved by selecting more correspondence points.

Due to differences in exposure between the images, the mask leaves a clear seam where the images overlap. I decided to "feather" my masks by having my left mask fall off linearly toward the right, and my right mask fall off linearly toward the left. Alhough this still leaves some faint wedges, the mask is less noticeable and the mosaic is pretty improved overall.

I used the same technique to blend the following images together.

Overview

For the second part of the project, I

Section I: Detecting Corner Features in an Image

Using the skeleton code, I computed the set of Harris interest points for each image. The initial set of points is very dense, an issue that we will address through adaptive non-maximal suppression. I also performed some initial thresholding by editing parameters from the skeleton code.

Section II: Adaptive Non-Maximal Suppression

To implement adaptive non-maximal suppression, I calculated an r value for each interest point according to the following equation:

The r value is the minimum distance from a point to its neighbor, where the h value of the point is at least 0.9 * the h value of the neighbor. Then, I selected the 500 points with the highest r values and discarded the rest. The suppressed points are more evenly distributed throughout the image and tend to fall along strong corners.

Section III: Extracting Feature Descriptors

Next, I sampled a 40x40 window around each interest point to obtain feature descriptors for the images. Each window was blurred and scaled down to an 8x8 patch, reducing the size of the vectors from 160 to 64 features. Finally, the patches were bias/gain-normalized.

Section IV: Matching Feature Descriptors

Using the descriptors obtained in the previous section, I identified features that were likely to be good matches during image stitching. After feature-matching, the remaining points are shared between the images.

I iterated through each feature from the first image and computed its SSD with each feature from the second image, keeping track of the first and second nearest-neighbor features. Next, I used Lowe's ratio test to determine if a feature and its first nearest-neighbor were matching. If the ratio between the SSDs of the first nearest-neighbor and the second nearest-neighbor lay below a certain threshold (which I ranged between 0.2 to 0.3 based on the paper), I considered the pair a match, as the first nearest-neighbor was much closer than the second nearest-neighbor.

Section V: Computing Robust Homographies

Finally, I implemented RANSAC, a method for computing homographies that minimizes the effect of outliers. My RANSAC loop ran 100 times and selected four random pairs of features at each step. I computed a homography from each set of features, using it to warp all of the points from the source image. I then iterated through the warped points to identify inliers, warped points that end up less than 4 pixels away from the target point. I kept track of the largest set of inliers and used it to compute the final homography at the end of the function.

I used the warping methods from the previous part of the project along with the new methods to automate the image-stitching process.

I auto-stitched the rest of the images as well.

The results are comparable to the hand-stitched mosaics, though the hand-stitched ones are a little better across the board.

Conclusion

The coolest thing I learned was how we were able to automate image-stitching—a normally time-intensive process—with just a few helper functions. I wonder how we can apply some of the concepts from this project to automating other computer vision tasks.